Einleitung
Ich weiß, unter Halbwertsentfernung kann man sich schlecht etwas vorstellen, der Begriff erinnert an die Halbwertszeit und ist auch etwas Ähnliches. Ich versuche, ihn mal zu erklären, auch wenn dazu etwas Mathematik nötig ist.
Eine halbe Bier enthält in München 0,5 l, in Nürnberg nur noch 0,4l. Die Entfernung München-Nürnberg beträgt rund 160km. Man könnte nun annehmen, dass die Größe der Biergläser nach Norden hin auf 160km um 0,1l abnimmt. Dann müssten aber die Biergläser in Gegenden, die mehr als 5x160km=800km nördlich von München liegen, negativen Rauminhalt haben, also konvexe Form haben. Das widerspricht aber dem Wesen eines Flüssigkeitsbehälters.
Herleitung
Offensichtlich handelt es sich bei der Volumenänderung der Biergläser nicht um eine lineare sondern um eine exponentielle Abnahme. Und da jede exponentielle Abnahme dem radioaktiven Zerfall gleicht, lässt sich ausrechnen, in welcher Entfernung zum Ausgangsort die Biergläser nur noch halb so groß sind. Hier die Herleitung auch für mathematisch Unbegabte:
Nach 160 km nimmt das Volumen von 0,5l auf 0,4l also um 20% ab, hat also nur noch 80%.
n gibt also den Faktor an, der mit 160km multipliziert werden muss, so dass in der Entfernung die Biergläser nur noch das halbe Volumen haben.
Für Köln ergibt sich bei einem Abstand zu München von 580km mit dieser Rechnung ein Wert von 0,22l. Praktischerweise runden die Kölner diesen Wert auf 0,2l herab, was nun bedeutet, dass in Köln das Bier in Behältnissen ausgeschenkt wird, die Reagenzgläsern nicht unähnlich sind. Da dort nun auch die Biereinheit in 0,2l berechnet wird, kann sich ein geübter und spendabler Biertrinker um den Bierdeckel herum trinken, was ihm in München trotz eisernen Trainings nie gelingen wird.

0,5 x 0,8n = 0,25
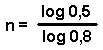
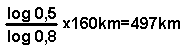
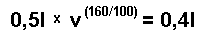
daraus folgt


Bei mir klappt es, seit ich diese Eselsbrücke gelesen habe:
Wird ihr Bauch konvex,
Ist das Mädchen brav,
Bleibt ihr Bauch konkav.